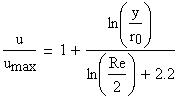In this case (round pipe flow) control authority would
be limited by 4-5%.
However, in assumption that the DPZTFFC will change
interaction between flow and wall surface we can change
the velocity to make flow turbulent earlier. For example,
for pipe with 10 mm dia. and water as media Re~10^4*V
and critical velocity is 0.2 m/sec. Presumably the
DPZTFFC could make the critical velocity smaller.
In this case ( laminar / turbulent flow transfer) control
authority would be 50-80% of flow.